This is a static, non-editable tutorial.
We recommend you install QuCumber if you want to run the examples locally.
You can then get an archive file containing the examples from the relevant release
here.
Alternatively, you can launch an interactive online version, though it may be a bit slow:
Reconstruction of a complex wavefunction¶
In this tutorial, a walkthrough of how to reconstruct a complex wavefunction via training a Restricted Boltzmann Machine (RBM), the neural network behind QuCumber, will be presented.
The wavefunction to be reconstructed¶
The simple wavefunction below describing two qubits (coefficients stored in qubits_psi.txt) will be reconstructed.
where the exact values of and
used for this tutorial are
The example dataset, qubits_train.txt, comprises of 500 measurements made in various bases (X, Y and Z). A corresponding file containing the bases for each data point in
qubits_train.txt, qubits_train_bases.txt, is also required. As per convention, spins are represented in binary notation with zero and one denoting spin-down and spin-up, respectively.
Using qucumber to reconstruct the wavefunction¶
Imports¶
To begin the tutorial, first import the required Python packages.
[1]:
import numpy as np
import torch
import matplotlib.pyplot as plt
from qucumber.nn_states import ComplexWaveFunction
from qucumber.callbacks import MetricEvaluator
import qucumber.utils.unitaries as unitaries
import qucumber.utils.cplx as cplx
import qucumber.utils.training_statistics as ts
import qucumber.utils.data as data
The Python class ComplexWaveFunction contains generic properties of a RBM meant to reconstruct a complex wavefunction, the most notable one being the gradient function required for stochastic gradient descent.
To instantiate a ComplexWaveFunction object, one needs to specify the number of visible and hidden units in the RBM. The number of visible units, num_visible, is given by the size of the physical system, i.e. the number of spins or qubits (2 in this case), while the number of hidden units, num_hidden, can be varied to change the expressiveness of the neural network.
Note: The optimal num_hidden : num_visible ratio will depend on the system. For the two-qubit wavefunction described above, good results can be achieved when this ratio is 1.
On top of needing the number of visible and hidden units, a ComplexWaveFunction object requires the user to input a dictionary containing the unitary operators (2x2) that will be used to rotate the qubits in and out of the computational basis, Z, during the training process. The unitaries utility will take care of creating this dictionary.
The MetricEvaluator class and training_statistics utility are built-in amenities that will allow the user to evaluate the training in real time.
Lastly, the cplx utility allows QuCumber to be able to handle complex numbers. Currently, PyTorch does not support complex numbers.
Training¶
To evaluate the training in real time, the fidelity between the true wavefunction of the system and the wavefunction that QuCumber reconstructs, , will be calculated along with the Kullback-Leibler (KL) divergence (the RBM’s cost function). First, the training data and the true wavefunction of this system need to be loaded using the
data utility.
[2]:
train_path = "qubits_train.txt"
train_bases_path = "qubits_train_bases.txt"
psi_path = "qubits_psi.txt"
bases_path = "qubits_bases.txt"
train_samples, true_psi, train_bases, bases = data.load_data(
train_path, psi_path, train_bases_path, bases_path
)
The file qubits_bases.txt contains every unique basis in the qubits_train_bases.txt file. Calculation of the full KL divergence in every basis requires the user to specify each unique basis.
As previously mentioned, a ComplexWaveFunction object requires a dictionary that contains the unitary operators that will be used to rotate the qubits in and out of the computational basis, Z, during the training process. In the case of the provided dataset, the unitaries required are the well-known , and
gates. The dictionary needed can be created with the following command.
[3]:
unitary_dict = unitaries.create_dict()
# unitary_dict = unitaries.create_dict(unitary_name=torch.tensor([[real part],
# [imaginary part]],
# dtype=torch.double)
If the user wishes to add their own unitary operators from their experiment to unitary_dict, uncomment the block above. When unitaries.create_dict() is called, it will contain the identity and the and
gates by default under the keys “Z”, “X” and “Y”, respectively.
The number of visible units in the RBM is equal to the number of qubits. The number of hidden units will also be taken to be the number of visible units.
[4]:
nv = train_samples.shape[-1]
nh = nv
nn_state = ComplexWaveFunction(
num_visible=nv, num_hidden=nh, unitary_dict=unitary_dict, gpu=False
)
By default, QuCumber will attempt to run on a GPU if one is available (if one is not available, QuCumber will fall back to CPU). If one wishes to guarantee that QuCumber runs on the CPU, add the flag gpu=False in the ComplexWaveFunction object instantiation. Set gpu=True in the line above to run this tutorial on a GPU.
Now the hyperparameters of the training process can be specified.
epochs: the total number of training cycles that will be performed (default = 100)pos_batch_size: the number of data points used in the positive phase of the gradient (default = 100)neg_batch_size: the number of data points used in the negative phase of the gradient (default =pos_batch_size)k: the number of contrastive divergence steps (default = 1)lr: the learning rate (default = 0.001)Note: For more information on the hyperparameters above, it is strongly encouraged that the user to read through the brief, but thorough theory document on RBMs. One does not have to specify these hyperparameters, as their default values will be used without the user overwriting them. It is recommended to keep with the default values until the user has a stronger grasp on what these hyperparameters mean. The quality and the computational efficiency of the training will highly depend on the choice of hyperparameters. As such, playing around with the hyperparameters is almost always necessary.
The two-qubit example in this tutorial should be extremely easy to train, regardless of the choice of hyperparameters. However, the hyperparameters below will be used.
[5]:
epochs = 100
pbs = 50 # pos_batch_size
nbs = 50 # neg_batch_size
lr = 0.1
k = 5
For evaluating the training in real time, the MetricEvaluator will be called to calculate the training evaluators every 10 epochs. The MetricEvaluator requires the following arguments.
period: the frequency of the training evaluators being calculated (e.g.period=200means that theMetricEvaluatorwill compute the desired metrics every 200 epochs)A dictionary of functions you would like to reference to evaluate the training (arguments required for these functions are keyword arguments placed after the dictionary)
The following additional arguments are needed to calculate the fidelity and KL divergence in the training_statistics utility.
target_psi(the true wavefunction of the system)space(the entire Hilbert space of the system)
The training evaluators can be printed out via the verbose=True statement.
Although the fidelity and KL divergence are excellent training evaluators, they are not practical to calculate in most cases; the user may not have access to the target wavefunction of the system, nor may generating the Hilbert space of the system be computationally feasible. However, evaluating the training in real time is extremely convenient.
Any custom function that the user would like to use to evaluate the training can be given to the MetricEvaluator, thus avoiding having to calculate fidelity and/or KL divergence. As an example, functions that calculate the the norm of each of the reconstructed wavefunction’s coefficients are presented. Any custom function given to MetricEvaluator must take the neural-network state (in this case, the ComplexWaveFunction object) and keyword arguments. Although the given example
requires the Hilbert space to be computed, the scope of the MetricEvaluator’s ability to be able to handle any function should still be evident.
[6]:
def alpha(nn_state, space, **kwargs):
rbm_psi = nn_state.psi(space)
normalization = nn_state.compute_normalization(space).sqrt_()
alpha_ = cplx.norm(
torch.tensor([rbm_psi[0][0], rbm_psi[1][0]], device=nn_state.device)
/ normalization
)
return alpha_
def beta(nn_state, space, **kwargs):
rbm_psi = nn_state.psi(space)
normalization = nn_state.compute_normalization(space).sqrt_()
beta_ = cplx.norm(
torch.tensor([rbm_psi[0][1], rbm_psi[1][1]], device=nn_state.device)
/ normalization
)
return beta_
def gamma(nn_state, space, **kwargs):
rbm_psi = nn_state.psi(space)
normalization = nn_state.compute_normalization(space).sqrt_()
gamma_ = cplx.norm(
torch.tensor([rbm_psi[0][2], rbm_psi[1][2]], device=nn_state.device)
/ normalization
)
return gamma_
def delta(nn_state, space, **kwargs):
rbm_psi = nn_state.psi(space)
normalization = nn_state.compute_normalization(space).sqrt_()
delta_ = cplx.norm(
torch.tensor([rbm_psi[0][3], rbm_psi[1][3]], device=nn_state.device)
/ normalization
)
return delta_
Now the Hilbert space of the system must be generated for the fidelity and KL divergence and the dictionary of functions the user would like to compute every period epochs must be given to the MetricEvaluator. Note that some of the coefficients aren’t being evaluated as they are commented out. This is simply to avoid cluttering the output, and may be uncommented by the user.
[7]:
period = 2
space = nn_state.generate_hilbert_space(nv)
callbacks = [
MetricEvaluator(
period,
{
"Fidelity": ts.fidelity,
"KL": ts.KL,
"normα": alpha,
# "normβ": beta,
# "normγ": gamma,
# "normδ": delta,
},
target_psi=true_psi,
bases=bases,
verbose=True,
space=space,
)
]
Now the training can begin. The ComplexWaveFunction object has a function called fit which takes care of this.
[8]:
nn_state.fit(
train_samples,
epochs=epochs,
pos_batch_size=pbs,
neg_batch_size=nbs,
lr=lr,
k=k,
input_bases=train_bases,
callbacks=callbacks,
)
Epoch: 2 Fidelity = 0.623747 KL = 0.226386 normα = 0.272518
Epoch: 4 Fidelity = 0.744691 KL = 0.142639 normα = 0.248872
Epoch: 6 Fidelity = 0.818254 KL = 0.094584 normα = 0.263589
Epoch: 8 Fidelity = 0.867098 KL = 0.067506 normα = 0.278453
Epoch: 10 Fidelity = 0.900217 KL = 0.051592 normα = 0.281094
Epoch: 12 Fidelity = 0.922993 KL = 0.041311 normα = 0.276052
Epoch: 14 Fidelity = 0.937807 KL = 0.034972 normα = 0.274676
Epoch: 16 Fidelity = 0.947232 KL = 0.030543 normα = 0.283873
Epoch: 18 Fidelity = 0.955277 KL = 0.027313 normα = 0.278906
Epoch: 20 Fidelity = 0.959930 KL = 0.025034 normα = 0.290271
Epoch: 22 Fidelity = 0.963333 KL = 0.023719 normα = 0.296183
Epoch: 24 Fidelity = 0.969419 KL = 0.021086 normα = 0.276108
Epoch: 26 Fidelity = 0.972300 KL = 0.020200 normα = 0.290305
Epoch: 28 Fidelity = 0.974777 KL = 0.018635 normα = 0.284231
Epoch: 30 Fidelity = 0.976208 KL = 0.017865 normα = 0.282036
Epoch: 32 Fidelity = 0.978382 KL = 0.016862 normα = 0.282498
Epoch: 34 Fidelity = 0.980578 KL = 0.015977 normα = 0.279435
Epoch: 36 Fidelity = 0.980983 KL = 0.015545 normα = 0.277835
Epoch: 38 Fidelity = 0.982651 KL = 0.014751 normα = 0.280070
Epoch: 40 Fidelity = 0.983155 KL = 0.014353 normα = 0.276912
Epoch: 42 Fidelity = 0.983996 KL = 0.013827 normα = 0.278844
Epoch: 44 Fidelity = 0.982731 KL = 0.015100 normα = 0.305219
Epoch: 46 Fidelity = 0.984791 KL = 0.013417 normα = 0.293674
Epoch: 48 Fidelity = 0.985395 KL = 0.012845 normα = 0.280658
Epoch: 50 Fidelity = 0.986767 KL = 0.012093 normα = 0.277599
Epoch: 52 Fidelity = 0.987795 KL = 0.011650 normα = 0.278886
Epoch: 54 Fidelity = 0.987057 KL = 0.011843 normα = 0.271735
Epoch: 56 Fidelity = 0.987125 KL = 0.011552 normα = 0.280304
Epoch: 58 Fidelity = 0.987295 KL = 0.011382 normα = 0.288229
Epoch: 60 Fidelity = 0.988201 KL = 0.011201 normα = 0.266736
Epoch: 62 Fidelity = 0.989181 KL = 0.010504 normα = 0.288520
Epoch: 64 Fidelity = 0.989308 KL = 0.010293 normα = 0.292218
Epoch: 66 Fidelity = 0.989321 KL = 0.009901 normα = 0.282069
Epoch: 68 Fidelity = 0.989347 KL = 0.009836 normα = 0.275723
Epoch: 70 Fidelity = 0.989494 KL = 0.009838 normα = 0.293840
Epoch: 72 Fidelity = 0.990115 KL = 0.009225 normα = 0.282556
Epoch: 74 Fidelity = 0.990199 KL = 0.009095 normα = 0.278911
Epoch: 76 Fidelity = 0.989979 KL = 0.009214 normα = 0.273241
Epoch: 78 Fidelity = 0.989633 KL = 0.009275 normα = 0.274384
Epoch: 80 Fidelity = 0.989972 KL = 0.008976 normα = 0.275430
Epoch: 82 Fidelity = 0.989920 KL = 0.008871 normα = 0.285605
Epoch: 84 Fidelity = 0.991177 KL = 0.008183 normα = 0.282607
Epoch: 86 Fidelity = 0.991249 KL = 0.008095 normα = 0.276934
Epoch: 88 Fidelity = 0.990857 KL = 0.008273 normα = 0.272151
Epoch: 90 Fidelity = 0.990802 KL = 0.008071 normα = 0.280823
Epoch: 92 Fidelity = 0.991090 KL = 0.007838 normα = 0.279963
Epoch: 94 Fidelity = 0.990995 KL = 0.007861 normα = 0.275772
Epoch: 96 Fidelity = 0.990326 KL = 0.008202 normα = 0.289882
Epoch: 98 Fidelity = 0.991012 KL = 0.007690 normα = 0.277037
Epoch: 100 Fidelity = 0.991736 KL = 0.007292 normα = 0.275516
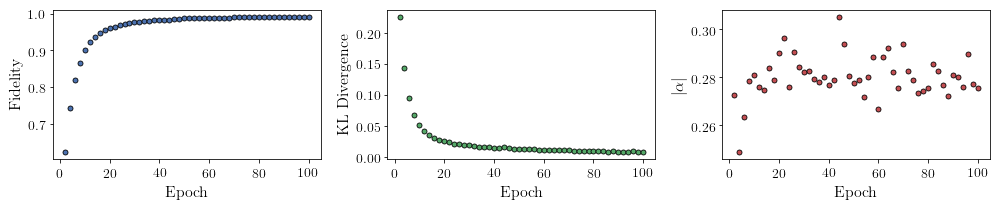
All of these training evaluators can be accessed after the training has completed, as well. The code below shows this, along with plots of each training evaluator versus the training cycle number (epoch).
[9]:
# Note that the key given to the *MetricEvaluator* must be
# what comes after callbacks[0].
fidelities = callbacks[0].Fidelity
# Alternatively, we may use the usual dictionary/list subscripting
# syntax. This is useful in cases where the name of the metric
# may contain special characters or spaces.
KLs = callbacks[0]["KL"]
coeffs = callbacks[0]["normα"]
epoch = np.arange(period, epochs + 1, period)
[10]:
# Some parameters to make the plots look nice
params = {
"text.usetex": True,
"font.family": "serif",
"legend.fontsize": 14,
"figure.figsize": (10, 3),
"axes.labelsize": 16,
"xtick.labelsize": 14,
"ytick.labelsize": 14,
"lines.linewidth": 2,
"lines.markeredgewidth": 0.8,
"lines.markersize": 5,
"lines.marker": "o",
"patch.edgecolor": "black",
}
plt.rcParams.update(params)
plt.style.use("seaborn-deep")
[11]:
fig, axs = plt.subplots(nrows=1, ncols=3, figsize=(14, 3))
ax = axs[0]
ax.plot(epoch, fidelities, "o", color="C0", markeredgecolor="black")
ax.set_ylabel(r"Fidelity")
ax.set_xlabel(r"Epoch")
ax = axs[1]
ax.plot(epoch, KLs, "o", color="C1", markeredgecolor="black")
ax.set_ylabel(r"KL Divergence")
ax.set_xlabel(r"Epoch")
ax = axs[2]
ax.plot(epoch, coeffs, "o", color="C2", markeredgecolor="black")
ax.set_ylabel(r"$\vert\alpha\vert$")
ax.set_xlabel(r"Epoch")
plt.tight_layout()
plt.savefig("complex_fid_KL.pdf")
plt.show()
It should be noted that one could have just ran nn_state.fit(train_samples) and just used the default hyperparameters and no training evaluators.
At the end of the training process, the network parameters (the weights, visible biases and hidden biases) are stored in the ComplexWaveFunction object. One can save them to a pickle file, which will be called saved_params.pt, with the following command.
[12]:
nn_state.save("saved_params.pt")
This saves the weights, visible biases and hidden biases as torch tensors with the following keys: “weights”, “visible_bias”, “hidden_bias”.