This is a static, non-editable tutorial.
We recommend you install QuCumber if you want to run the examples locally.
You can then get an archive file containing the examples from the relevant release
here.
Alternatively, you can launch an interactive online version, though it may be a bit slow:
Reconstruction of a positive-real wavefunction¶
This tutorial shows how to reconstruct a positive-real wavefunction via training a Restricted Boltzmann Machine (RBM), the neural network behind QuCumber. The data used for training are measurements from a one-dimensional transverse-field Ising model (TFIM) with 10 sites at its critical point.
Transverse-field Ising model¶
The example dataset, located in tfim1d_data.txt, comprises 10,000 measurements from a one-dimensional TFIM with 10 sites at its critical point. The Hamiltonian for the TFIM is given by
where is the conventional spin-1/2 Pauli operator on site
. At the critical point,
. By convention, spins are represented in binary notation with zero and one denoting the states spin-down and spin-up, respectively.
Using QuCumber to reconstruct the wavefunction¶
Imports¶
To begin the tutorial, first import the required Python packages.
[1]:
import numpy as np
import matplotlib.pyplot as plt
from qucumber.nn_states import PositiveWaveFunction
from qucumber.callbacks import MetricEvaluator
import qucumber.utils.training_statistics as ts
import qucumber.utils.data as data
The Python class PositiveWaveFunction contains generic properties of a RBM meant to reconstruct a positive-real wavefunction, the most notable one being the gradient function required for stochastic gradient descent.
To instantiate a PositiveWaveFunction object, one needs to specify the number of visible and hidden units in the RBM. The number of visible units, num_visible, is given by the size of the physical system, i.e. the number of spins or qubits (10 in this case), while the number of hidden units, num_hidden, can be varied to change the expressiveness of the neural network.
Note: The optimal num_hidden : num_visible ratio will depend on the system. For the TFIM, having this ratio be equal to 1 leads to good results with reasonable computational effort.
Training¶
To evaluate the training in real time, we compute the fidelity between the true ground-state wavefunction of the system and the wavefunction that QuCumber reconstructs, , along with the Kullback-Leibler (KL) divergence (the RBM’s cost function). As will be shown below, any custom function can be used to evaluate the training.
First, the training data and the true wavefunction of this system must be loaded using the data utility.
[2]:
psi_path = "tfim1d_psi.txt"
train_path = "tfim1d_data.txt"
train_data, true_psi = data.load_data(train_path, psi_path)
As previously mentioned, to instantiate a PositiveWaveFunction object, one needs to specify the number of visible and hidden units in the RBM; we choose them to be equal.
[3]:
nv = train_data.shape[-1]
nh = nv
nn_state = PositiveWaveFunction(num_visible=nv, num_hidden=nh)
# nn_state = PositiveWaveFunction(num_visible=nv, num_hidden=nh, gpu = False)
By default, QuCumber will attempt to run on a GPU, and default to CPU if GPU is not available. To run QuCumber on a CPU, add the flag gpu=False in the PositiveWaveFunction object instantiation (i.e. uncomment the line above).
Now we specify the hyperparameters of the training process:
epochs: the total number of training cycles that will be performed (default = 100)pbs(pos_batch_size): the number of data points used in the positive phase of the gradient (default = 100)nbs(neg_batch_size): the number of data points used in the negative phase of the gradient (default = 100)k: the number of contrastive divergence steps (default = 1)lr: the learning rate (default = 0.001)Note: For more information on the hyperparameters above, it is strongly encouraged that the user to read through the brief, but thorough theory document on RBMs located in the QuCumber documentation. One does not have to specify these hyperparameters, as their default values will be used without the user overwriting them. It is recommended to keep with the default values until the user has a stronger grasp on what these hyperparameters mean. The quality and the computational efficiency of the training will highly depend on the choice of hyperparameters. As such, playing around with the hyperparameters is almost always necessary.
For the TFIM with 10 sites, the following hyperparameters give excellent results:
[4]:
epochs = 500
pbs = 100
nbs = pbs
lr = 0.01
k = 10
For evaluating the training in real time, the MetricEvaluator is called every 100 epochs in order to calculate the training evaluators. The MetricEvaluator requires the following arguments:
period: the frequency of the training evaluators being calculated (e.g.period=100means that theMetricEvaluatorwill do an evaluation every 100 epochs)A dictionary of functions you would like to reference to evaluate the training (arguments required for these functions are keyword arguments placed after the dictionary)
The following additional arguments are needed to calculate the fidelity and KL divergence in the training_statistics utility:
target_psi: the true wavefunction of the systemspace: the Hilbert space of the system
The training evaluators can be printed out via the verbose=True statement.
Although the fidelity and KL divergence are excellent training evaluators, they are not practical to calculate in most cases; the user may not have access to the target wavefunction of the system, nor may generating the Hilbert space of the system be computationally feasible. However, evaluating the training in real time is extremely convenient.
Any custom function that the user would like to use to evaluate the training can be given to the MetricEvaluator, thus avoiding having to calculate fidelity and/or KL divergence. Any custom function given to MetricEvaluator must take the neural-network state (in this case, the PositiveWaveFunction object) and keyword arguments. As an example, we define a custom function psi_coefficient, which is the fifth coefficient of the reconstructed wavefunction multiplied by a parameter
.
[5]:
def psi_coefficient(nn_state, space, A, **kwargs):
norm = nn_state.compute_normalization(space).sqrt_()
return A * nn_state.psi(space)[0][4] / norm
Now the Hilbert space of the system can be generated for the fidelity and KL divergence.
[6]:
period = 10
space = nn_state.generate_hilbert_space(nv)
Now the training can begin. The PositiveWaveFunction object has a property called fit which takes care of this. MetricEvaluator must be passed to the fit function in a list (callbacks).
[7]:
callbacks = [
MetricEvaluator(
period,
{"Fidelity": ts.fidelity, "KL": ts.KL, "A_Ψrbm_5": psi_coefficient},
target_psi=true_psi,
verbose=True,
space=space,
A=3.0,
)
]
nn_state.fit(
train_data,
epochs=epochs,
pos_batch_size=pbs,
neg_batch_size=nbs,
lr=lr,
k=k,
callbacks=callbacks,
)
Epoch: 10 Fidelity = 0.526148 KL = 1.310731 A_Ψrbm_5 = 0.125463
Epoch: 20 Fidelity = 0.631814 KL = 0.875887 A_Ψrbm_5 = 0.193193
Epoch: 30 Fidelity = 0.736986 KL = 0.577408 A_Ψrbm_5 = 0.249697
Epoch: 40 Fidelity = 0.794626 KL = 0.445550 A_Ψrbm_5 = 0.267554
Epoch: 50 Fidelity = 0.828487 KL = 0.363523 A_Ψrbm_5 = 0.263156
Epoch: 60 Fidelity = 0.861033 KL = 0.284768 A_Ψrbm_5 = 0.255909
Epoch: 70 Fidelity = 0.888133 KL = 0.226607 A_Ψrbm_5 = 0.251317
Epoch: 80 Fidelity = 0.904473 KL = 0.191903 A_Ψrbm_5 = 0.230342
Epoch: 90 Fidelity = 0.916896 KL = 0.168523 A_Ψrbm_5 = 0.232834
Epoch: 100 Fidelity = 0.925543 KL = 0.151414 A_Ψrbm_5 = 0.226578
Epoch: 110 Fidelity = 0.933069 KL = 0.136249 A_Ψrbm_5 = 0.227657
Epoch: 120 Fidelity = 0.939533 KL = 0.122066 A_Ψrbm_5 = 0.216086
Epoch: 130 Fidelity = 0.945398 KL = 0.109634 A_Ψrbm_5 = 0.210336
Epoch: 140 Fidelity = 0.950329 KL = 0.099964 A_Ψrbm_5 = 0.214536
Epoch: 150 Fidelity = 0.954255 KL = 0.092397 A_Ψrbm_5 = 0.212398
Epoch: 160 Fidelity = 0.957539 KL = 0.086165 A_Ψrbm_5 = 0.213869
Epoch: 170 Fidelity = 0.959890 KL = 0.081415 A_Ψrbm_5 = 0.205124
Epoch: 180 Fidelity = 0.961762 KL = 0.077955 A_Ψrbm_5 = 0.207600
Epoch: 190 Fidelity = 0.963395 KL = 0.075018 A_Ψrbm_5 = 0.203214
Epoch: 200 Fidelity = 0.965103 KL = 0.071877 A_Ψrbm_5 = 0.207948
Epoch: 210 Fidelity = 0.966435 KL = 0.069428 A_Ψrbm_5 = 0.216086
Epoch: 220 Fidelity = 0.967274 KL = 0.067780 A_Ψrbm_5 = 0.215082
Epoch: 230 Fidelity = 0.968685 KL = 0.064706 A_Ψrbm_5 = 0.211092
Epoch: 240 Fidelity = 0.969841 KL = 0.062323 A_Ψrbm_5 = 0.213523
Epoch: 250 Fidelity = 0.971052 KL = 0.059850 A_Ψrbm_5 = 0.212783
Epoch: 260 Fidelity = 0.971965 KL = 0.057842 A_Ψrbm_5 = 0.208115
Epoch: 270 Fidelity = 0.973736 KL = 0.054289 A_Ψrbm_5 = 0.215748
Epoch: 280 Fidelity = 0.974085 KL = 0.053346 A_Ψrbm_5 = 0.212171
Epoch: 290 Fidelity = 0.976066 KL = 0.049299 A_Ψrbm_5 = 0.219986
Epoch: 300 Fidelity = 0.977303 KL = 0.046733 A_Ψrbm_5 = 0.225259
Epoch: 310 Fidelity = 0.978261 KL = 0.044790 A_Ψrbm_5 = 0.228821
Epoch: 320 Fidelity = 0.979351 KL = 0.042555 A_Ψrbm_5 = 0.225733
Epoch: 330 Fidelity = 0.980212 KL = 0.040565 A_Ψrbm_5 = 0.223765
Epoch: 340 Fidelity = 0.981664 KL = 0.037660 A_Ψrbm_5 = 0.226980
Epoch: 350 Fidelity = 0.982528 KL = 0.035918 A_Ψrbm_5 = 0.230829
Epoch: 360 Fidelity = 0.983351 KL = 0.034181 A_Ψrbm_5 = 0.224962
Epoch: 370 Fidelity = 0.984213 KL = 0.032504 A_Ψrbm_5 = 0.225617
Epoch: 380 Fidelity = 0.984872 KL = 0.031177 A_Ψrbm_5 = 0.227120
Epoch: 390 Fidelity = 0.985186 KL = 0.030594 A_Ψrbm_5 = 0.222515
Epoch: 400 Fidelity = 0.985662 KL = 0.029606 A_Ψrbm_5 = 0.220782
Epoch: 410 Fidelity = 0.986466 KL = 0.028079 A_Ψrbm_5 = 0.227727
Epoch: 420 Fidelity = 0.986970 KL = 0.027100 A_Ψrbm_5 = 0.233300
Epoch: 430 Fidelity = 0.987040 KL = 0.026978 A_Ψrbm_5 = 0.232759
Epoch: 440 Fidelity = 0.987675 KL = 0.025714 A_Ψrbm_5 = 0.224514
Epoch: 450 Fidelity = 0.988244 KL = 0.024636 A_Ψrbm_5 = 0.229669
Epoch: 460 Fidelity = 0.988569 KL = 0.023975 A_Ψrbm_5 = 0.230897
Epoch: 470 Fidelity = 0.988666 KL = 0.023802 A_Ψrbm_5 = 0.229378
Epoch: 480 Fidelity = 0.988781 KL = 0.023565 A_Ψrbm_5 = 0.236488
Epoch: 490 Fidelity = 0.989243 KL = 0.022694 A_Ψrbm_5 = 0.228858
Epoch: 500 Fidelity = 0.988991 KL = 0.023196 A_Ψrbm_5 = 0.235301
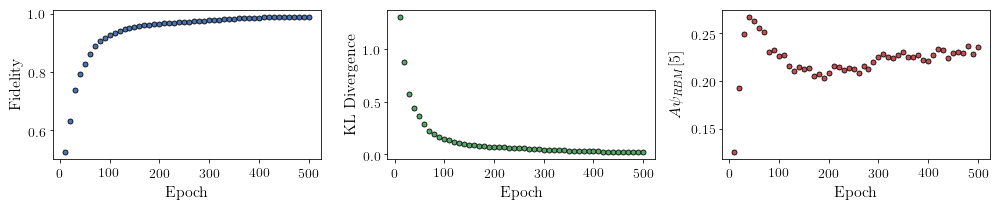
All of these training evaluators can be accessed after the training has completed. The code below shows this, along with plots of each training evaluator as a function of epoch (training cycle number).
[8]:
# Note that the key given to the *MetricEvaluator* must be
# what comes after callbacks[0].
fidelities = callbacks[0].Fidelity
# Alternatively, we can use the usual dictionary/list subsripting
# syntax. This is useful in cases where the name of the
# metric contains special characters or spaces.
KLs = callbacks[0]["KL"]
coeffs = callbacks[0]["A_Ψrbm_5"]
epoch = np.arange(period, epochs + 1, period)
[9]:
# Some parameters to make the plots look nice
params = {
"text.usetex": True,
"font.family": "serif",
"legend.fontsize": 14,
"figure.figsize": (10, 3),
"axes.labelsize": 16,
"xtick.labelsize": 14,
"ytick.labelsize": 14,
"lines.linewidth": 2,
"lines.markeredgewidth": 0.8,
"lines.markersize": 5,
"lines.marker": "o",
"patch.edgecolor": "black",
}
plt.rcParams.update(params)
plt.style.use("seaborn-deep")
[10]:
# Plotting
fig, axs = plt.subplots(nrows=1, ncols=3, figsize=(14, 3))
ax = axs[0]
ax.plot(epoch, fidelities, "o", color="C0", markeredgecolor="black")
ax.set_ylabel(r"Fidelity")
ax.set_xlabel(r"Epoch")
ax = axs[1]
ax.plot(epoch, KLs, "o", color="C1", markeredgecolor="black")
ax.set_ylabel(r"KL Divergence")
ax.set_xlabel(r"Epoch")
ax = axs[2]
ax.plot(epoch, coeffs, "o", color="C2", markeredgecolor="black")
ax.set_ylabel(r"$A\psi_{RBM}[5]$")
ax.set_xlabel(r"Epoch")
plt.tight_layout()
plt.savefig("fid_KL.pdf")
plt.show()
It should be noted that one could have just ran nn_state.fit(train_samples), which uses the default hyperparameters and no training evaluators.
To demonstrate how important it is to find the optimal hyperparameters for a certain system, restart this notebook and comment out the original fit statement, then uncomment and run the cell below.
[11]:
# nn_state.fit(train_samples)
Using the non-default hyperparameters yielded a fidelity of approximately , while the default hyperparameters yield approximately
!
The trained RBM’s parameters are saved to a pickle file with the name saved_params.pt for future use in other tutorials:
[12]:
nn_state.save("saved_params.pt")
This saves the weights, visible biases and hidden biases as torch tensors with the following keys: “weights”, “visible_bias”, “hidden_bias”.