This is a static, non-editable tutorial.
We recommend you install QuCumber if you want to run the examples locally.
You can then get an archive file containing the examples from the relevant release
here.
Alternatively, you can launch an interactive online version, though it may be a bit slow:
Reconstruction of a positive-real wavefunction¶
This tutorial shows how to reconstruct a positive-real wavefunction via training a Restricted Boltzmann Machine (RBM), the neural network behind QuCumber. The data used for training are measurements from a one-dimensional transverse-field Ising model (TFIM) with 10 sites at its critical point.
Transverse-field Ising model¶
The example dataset, located in tfim1d_data.txt, comprises 10,000 measurements from a one-dimensional TFIM with 10 sites at its critical point. The Hamiltonian for the TFIM is given by
where is the conventional spin-1/2 Pauli operator on site
. At the critical point,
. By convention, spins are represented in binary notation with zero and one denoting the states spin-down and spin-up, respectively.
Using QuCumber to reconstruct the wavefunction¶
Imports¶
To begin the tutorial, first import the required Python packages.
[1]:
import numpy as np
import matplotlib.pyplot as plt
from qucumber.nn_states import PositiveWaveFunction
from qucumber.callbacks import MetricEvaluator
import qucumber.utils.training_statistics as ts
import qucumber.utils.data as data
import qucumber
# set random seed on cpu but not gpu, since we won't use gpu for this tutorial
qucumber.set_random_seed(1234, cpu=True, gpu=False)
The Python class PositiveWaveFunction contains generic properties of a RBM meant to reconstruct a positive-real wavefunction, the most notable one being the gradient function required for stochastic gradient descent.
To instantiate a PositiveWaveFunction object, one needs to specify the number of visible and hidden units in the RBM. The number of visible units, num_visible, is given by the size of the physical system, i.e. the number of spins or qubits (10 in this case), while the number of hidden units, num_hidden, can be varied to change the expressiveness of the neural network.
Note: The optimal num_hidden : num_visible ratio will depend on the system. For the TFIM, having this ratio be equal to 1 leads to good results with reasonable computational effort.
Training¶
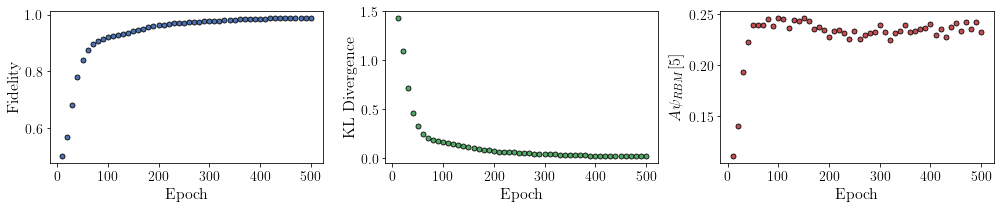
To evaluate the training in real time, we compute the fidelity between the true ground-state wavefunction of the system and the wavefunction that QuCumber reconstructs, , along with the Kullback-Leibler (KL) divergence (the RBM’s cost function). As will be shown below, any custom function can be used to evaluate the training.
First, the training data and the true wavefunction of this system must be loaded using the data utility.
[2]:
psi_path = "tfim1d_psi.txt"
train_path = "tfim1d_data.txt"
train_data, true_psi = data.load_data(train_path, psi_path)
As previously mentioned, to instantiate a PositiveWaveFunction object, one needs to specify the number of visible and hidden units in the RBM; we choose them to be equal.
[3]:
nv = train_data.shape[-1]
nh = nv
nn_state = PositiveWaveFunction(num_visible=nv, num_hidden=nh, gpu=False)
If gpu=True (the default), QuCumber will attempt to run on a GPU if one is available (otherwise, QuCumber will default to CPU). If one gpu=False, QuCumber will run on the CPU.
Now we specify the hyperparameters of the training process:
epochs: the total number of training cycles that will be performed (default = 100)pbs(pos_batch_size): the number of data points used in the positive phase of the gradient (default = 100)nbs(neg_batch_size): the number of data points used in the negative phase of the gradient (default = 100)k: the number of contrastive divergence steps (default = 1)lr: the learning rate (default = 0.001)Note: For more information on the hyperparameters above, it is strongly encouraged that the user to read through the brief, but thorough theory document on RBMs located in the QuCumber documentation. One does not have to specify these hyperparameters, as their default values will be used without the user overwriting them. It is recommended to keep with the default values until the user has a stronger grasp on what these hyperparameters mean. The quality and the computational efficiency of the training will highly depend on the choice of hyperparameters. As such, playing around with the hyperparameters is almost always necessary.
For the TFIM with 10 sites, the following hyperparameters give excellent results:
[4]:
epochs = 500
pbs = 100
nbs = pbs
lr = 0.01
k = 10
For evaluating the training in real time, the MetricEvaluator is called every 100 epochs in order to calculate the training evaluators. The MetricEvaluator requires the following arguments:
period: the frequency of the training evaluators being calculated (e.g.period=100means that theMetricEvaluatorwill do an evaluation every 100 epochs)A dictionary of functions you would like to reference to evaluate the training (arguments required for these functions are keyword arguments placed after the dictionary)
The following additional arguments are needed to calculate the fidelity and KL divergence in the training_statistics utility:
target_psi: the true wavefunction of the systemspace: the Hilbert space of the system
The training evaluators can be printed out via the verbose=True statement.
Although the fidelity and KL divergence are excellent training evaluators, they are not practical to calculate in most cases; the user may not have access to the target wavefunction of the system, nor may generating the Hilbert space of the system be computationally feasible. However, evaluating the training in real time is extremely convenient.
Any custom function that the user would like to use to evaluate the training can be given to the MetricEvaluator, thus avoiding having to calculate fidelity and/or KL divergence. Any custom function given to MetricEvaluator must take the neural-network state (in this case, the PositiveWaveFunction object) and keyword arguments. As an example, we define a custom function psi_coefficient, which is the fifth coefficient of the reconstructed wavefunction multiplied by a parameter
.
[5]:
def psi_coefficient(nn_state, space, A, **kwargs):
norm = nn_state.compute_normalization(space).sqrt_()
return A * nn_state.psi(space)[0][4] / norm
Now the Hilbert space of the system can be generated for the fidelity and KL divergence.
[6]:
period = 10
space = nn_state.generate_hilbert_space()
Now the training can begin. The PositiveWaveFunction object has a property called fit which takes care of this. MetricEvaluator must be passed to the fit function in a list (callbacks).
[7]:
callbacks = [
MetricEvaluator(
period,
{"Fidelity": ts.fidelity, "KL": ts.KL, "A_Ψrbm_5": psi_coefficient},
target=true_psi,
verbose=True,
space=space,
A=3.0,
)
]
nn_state.fit(
train_data,
epochs=epochs,
pos_batch_size=pbs,
neg_batch_size=nbs,
lr=lr,
k=k,
callbacks=callbacks,
time=True,
)
Epoch: 10 Fidelity = 0.500444 KL = 1.434037 A_Ψrbm_5 = 0.111008
Epoch: 20 Fidelity = 0.570243 KL = 1.098804 A_Ψrbm_5 = 0.140842
Epoch: 30 Fidelity = 0.681689 KL = 0.712384 A_Ψrbm_5 = 0.192823
Epoch: 40 Fidelity = 0.781095 KL = 0.457683 A_Ψrbm_5 = 0.222722
Epoch: 50 Fidelity = 0.840074 KL = 0.326949 A_Ψrbm_5 = 0.239039
Epoch: 60 Fidelity = 0.875057 KL = 0.252105 A_Ψrbm_5 = 0.239344
Epoch: 70 Fidelity = 0.895826 KL = 0.211282 A_Ψrbm_5 = 0.239159
Epoch: 80 Fidelity = 0.907819 KL = 0.190410 A_Ψrbm_5 = 0.245369
Epoch: 90 Fidelity = 0.914834 KL = 0.177129 A_Ψrbm_5 = 0.238663
Epoch: 100 Fidelity = 0.920255 KL = 0.167432 A_Ψrbm_5 = 0.246280
Epoch: 110 Fidelity = 0.924585 KL = 0.158587 A_Ψrbm_5 = 0.244731
Epoch: 120 Fidelity = 0.928158 KL = 0.150159 A_Ψrbm_5 = 0.236318
Epoch: 130 Fidelity = 0.932489 KL = 0.140405 A_Ψrbm_5 = 0.243707
Epoch: 140 Fidelity = 0.936930 KL = 0.130399 A_Ψrbm_5 = 0.242923
Epoch: 150 Fidelity = 0.941502 KL = 0.120001 A_Ψrbm_5 = 0.246340
Epoch: 160 Fidelity = 0.946511 KL = 0.108959 A_Ψrbm_5 = 0.243519
Epoch: 170 Fidelity = 0.951172 KL = 0.098144 A_Ψrbm_5 = 0.235464
Epoch: 180 Fidelity = 0.955645 KL = 0.088780 A_Ψrbm_5 = 0.237005
Epoch: 190 Fidelity = 0.959723 KL = 0.080219 A_Ψrbm_5 = 0.234366
Epoch: 200 Fidelity = 0.962512 KL = 0.074663 A_Ψrbm_5 = 0.227764
Epoch: 210 Fidelity = 0.965615 KL = 0.068804 A_Ψrbm_5 = 0.233611
Epoch: 220 Fidelity = 0.967394 KL = 0.065302 A_Ψrbm_5 = 0.233936
Epoch: 230 Fidelity = 0.969286 KL = 0.061641 A_Ψrbm_5 = 0.230911
Epoch: 240 Fidelity = 0.970506 KL = 0.059283 A_Ψrbm_5 = 0.225389
Epoch: 250 Fidelity = 0.971461 KL = 0.057742 A_Ψrbm_5 = 0.233186
Epoch: 260 Fidelity = 0.973525 KL = 0.053430 A_Ψrbm_5 = 0.225180
Epoch: 270 Fidelity = 0.975005 KL = 0.050646 A_Ψrbm_5 = 0.228983
Epoch: 280 Fidelity = 0.976041 KL = 0.048451 A_Ψrbm_5 = 0.231805
Epoch: 290 Fidelity = 0.977197 KL = 0.046058 A_Ψrbm_5 = 0.232667
Epoch: 300 Fidelity = 0.977386 KL = 0.045652 A_Ψrbm_5 = 0.239462
Epoch: 310 Fidelity = 0.979153 KL = 0.042036 A_Ψrbm_5 = 0.232371
Epoch: 320 Fidelity = 0.979264 KL = 0.041764 A_Ψrbm_5 = 0.224176
Epoch: 330 Fidelity = 0.981203 KL = 0.037786 A_Ψrbm_5 = 0.231017
Epoch: 340 Fidelity = 0.982122 KL = 0.035848 A_Ψrbm_5 = 0.233144
Epoch: 350 Fidelity = 0.982408 KL = 0.035287 A_Ψrbm_5 = 0.239080
Epoch: 360 Fidelity = 0.983737 KL = 0.032537 A_Ψrbm_5 = 0.232325
Epoch: 370 Fidelity = 0.984651 KL = 0.030705 A_Ψrbm_5 = 0.233523
Epoch: 380 Fidelity = 0.985230 KL = 0.029546 A_Ψrbm_5 = 0.235031
Epoch: 390 Fidelity = 0.985815 KL = 0.028345 A_Ψrbm_5 = 0.235860
Epoch: 400 Fidelity = 0.986262 KL = 0.027459 A_Ψrbm_5 = 0.240407
Epoch: 410 Fidelity = 0.986678 KL = 0.026623 A_Ψrbm_5 = 0.229870
Epoch: 420 Fidelity = 0.987422 KL = 0.025197 A_Ψrbm_5 = 0.235147
Epoch: 430 Fidelity = 0.987339 KL = 0.025400 A_Ψrbm_5 = 0.227832
Epoch: 440 Fidelity = 0.988037 KL = 0.023930 A_Ψrbm_5 = 0.237405
Epoch: 450 Fidelity = 0.988104 KL = 0.023838 A_Ψrbm_5 = 0.241163
Epoch: 460 Fidelity = 0.988751 KL = 0.022605 A_Ψrbm_5 = 0.233818
Epoch: 470 Fidelity = 0.988836 KL = 0.022364 A_Ψrbm_5 = 0.241944
Epoch: 480 Fidelity = 0.989127 KL = 0.021844 A_Ψrbm_5 = 0.235669
Epoch: 490 Fidelity = 0.989361 KL = 0.021288 A_Ψrbm_5 = 0.242225
Epoch: 500 Fidelity = 0.989816 KL = 0.020486 A_Ψrbm_5 = 0.232313
Total time elapsed during training: 87.096 s
All of these training evaluators can be accessed after the training has completed. The code below shows this, along with plots of each training evaluator as a function of epoch (training cycle number).
[8]:
# Note that the key given to the *MetricEvaluator* must be
# what comes after callbacks[0].
fidelities = callbacks[0].Fidelity
# Alternatively, we can use the usual dictionary/list subsripting
# syntax. This is useful in cases where the name of the
# metric contains special characters or spaces.
KLs = callbacks[0]["KL"]
coeffs = callbacks[0]["A_Ψrbm_5"]
epoch = np.arange(period, epochs + 1, period)
[9]:
# Some parameters to make the plots look nice
params = {
"text.usetex": True,
"font.family": "serif",
"legend.fontsize": 14,
"figure.figsize": (10, 3),
"axes.labelsize": 16,
"xtick.labelsize": 14,
"ytick.labelsize": 14,
"lines.linewidth": 2,
"lines.markeredgewidth": 0.8,
"lines.markersize": 5,
"lines.marker": "o",
"patch.edgecolor": "black",
}
plt.rcParams.update(params)
plt.style.use("seaborn-deep")
[10]:
# Plotting
fig, axs = plt.subplots(nrows=1, ncols=3, figsize=(14, 3))
ax = axs[0]
ax.plot(epoch, fidelities, "o", color="C0", markeredgecolor="black")
ax.set_ylabel(r"Fidelity")
ax.set_xlabel(r"Epoch")
ax = axs[1]
ax.plot(epoch, KLs, "o", color="C1", markeredgecolor="black")
ax.set_ylabel(r"KL Divergence")
ax.set_xlabel(r"Epoch")
ax = axs[2]
ax.plot(epoch, coeffs, "o", color="C2", markeredgecolor="black")
ax.set_ylabel(r"$A\psi_{RBM}[5]$")
ax.set_xlabel(r"Epoch")
plt.tight_layout()
plt.show()
It should be noted that one could have just ran nn_state.fit(train_samples), which uses the default hyperparameters and no training evaluators.
To demonstrate how important it is to find the optimal hyperparameters for a certain system, restart this notebook and comment out the original fit statement, then uncomment and run the cell below.
[11]:
# nn_state.fit(train_samples)
Using the non-default hyperparameters produced a fidelity of approximately , while the default hyperparameters yield approximately
!
The trained RBM can be saved to a pickle file with the name saved_params.pt for future use:
[12]:
nn_state.save("saved_params.pt")
This saves the weights, visible biases and hidden biases as torch tensors under the following keys: weights, visible_bias, hidden_bias.